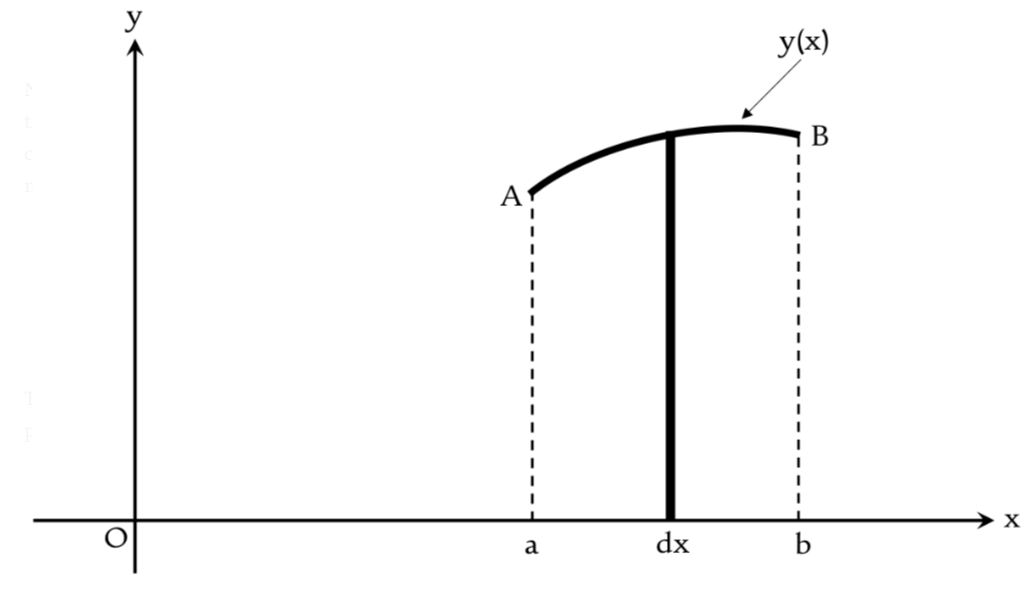
Figure 1: A rectangle with infinitesimal base dx and varying height y(x).
On November 11, 1675, German mathematician and polymath Gottfried Wilhelm Leibniz uses integral calculus for the first time to calculate the area under the graph of y = (x). Integral calculus is a subset of infinitesimal calculus, which also includes differential calculus. In general, infinitesimal calculus is the branch of mathematics that deals with tangent lines to curves, areas under curves, minima and maxima, and other geometric and analytic problems.

Figure 1 shows the area beneath the curve AB which was considered by Leibniz to be a sum of infinitely many rectangles with infinitesimal bases dx and varying height y(x).
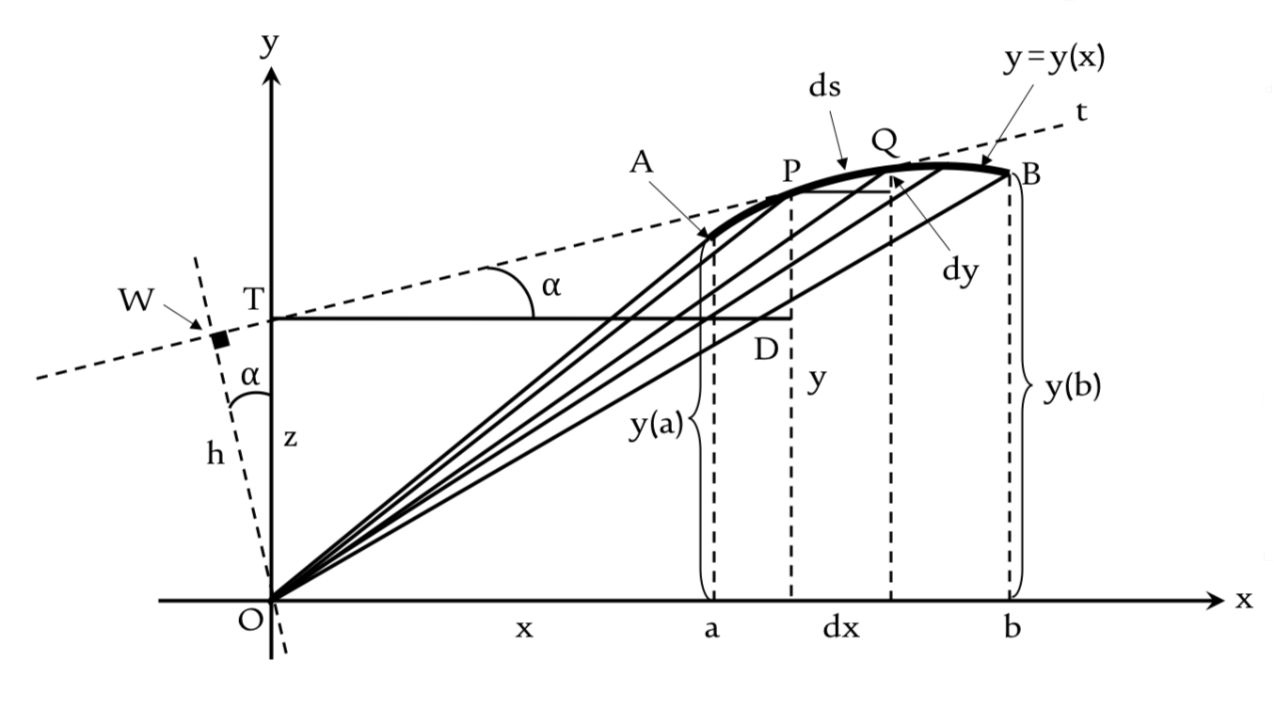
This convoluted construction shown in figure 2 yields one of the most commonly used calculus formulas, the integration by parts.
To see how a particular case of Leibniz's Transmutation theorem gives us the famous formula for the integration by parts, follow the link The Calculus according to Leibniz.